1. 알아보기
현시점 딥러닝 자연어 처리 분야에서 SOTA(State of the art)를 차지하는 기술의 시초가 되는 Transformer에 대해 알아보자.
Transformer는 2017년, Google이 낸 논문 Attention Is All You Need를 통해 세상에 이름을 알렸다.
Attention is all you need 논문
https://proceedings.neurips.cc/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf
Transformer가 제시된 논문 제목에서 알 수 있듯, Transformer에 대해 알기 위해선 먼저 Attention mechanism이 무엇인지에 대해 알아야 한다.
Attention mechanism에 대한 포스트를 추후 작성한 후 아래에 링크해 놓겠다.
Attention for seq2seq in python
간단하게 요약하면 Attention은 RNN 기반 seq2seq 모델의 장기 의존성(Long-term dependency) 문제를 해결하기 위해 고안된 방식이다.
기계번역과 같은 일을 수행하는 인공지능은 주로 RNN 기반의 LSTM을 사용해서 seq2seq 모델을 설계해왔다.
이 모델의 경우 인코더에서 디코더로 context vector라는 결과를 넘겨주는데, 디코더는 이 context vector를 바탕으로 결과를 출력한다.
다만, 고정된 크기의 context vector 하나로 인코더의 모든 단어와 맥락을 압축해서 전달해야 하기 때문에, 문장의 길이가 길어질수록 context vector에 문장 앞에서 쓰인 단어의 의미를 제대로 반영할 수 없다는 문제가 발생한다.
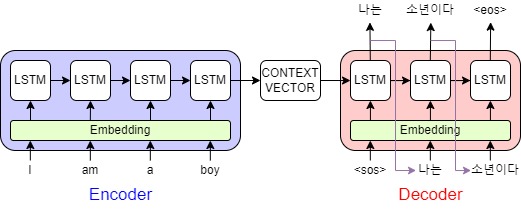
물론 위와 같은 seq2seq 모델에서 모든 입력에 대한 정보가 context vector에 담기기는 어렵지 않다. 하지만 한 문장에 단어가 엄청 많아진다면 LSTM을 계속 거치면서 앞부분에 나오는 단어의 의미가 디코더까지 잘 전달되지 못한다.
그래서 Attention이라는 새로운 방식이 고안되었다.
Attention은 인코더의 개별 출력을 보관하고 있다가 디코더에서 출력을 결정할 때 가중치를 주기 위해 사용한다.
Quary, Key, Value 방식으로, 검색엔진에서 검색하는 방식과 유사하다고 한다.

이런 식으로 인코더의 최종 출력인 context vector 뿐 아니라 각 출력 값을 저장해 뒀다가 Key, Value로 사용해서 디코더의 각 출력을 받아 계산 한 이후 다시 디코더의 출력과 합쳐서 결과를 출력하는 방식이다.
이게 효과가 좋았고 RNN 기반 자연어 처리의 정확도를 올려주는데 큰 공헌을 했다고 한다.
하지만 여전히 RNN 기반 자연어 처리에는 큰 문제가 있다.
바로 시간에 따라 계산되기 때문에 병렬 처리가 제대로 되지 않는다는 것.
딥러닝이 다시금 각광받게 된 이유에 빼놓을 수 없는 가장 큰 부분이 GPU를 통한 병렬 연산이라고 말할 수 있지만, Transformer 이전 RNN 기반 자연어 처리 모델은 입력 데이터에서 피쳐를 하나씩 넣어야 했기에 이러한 강점을 제대로 누릴 수 없었다.
2. Transformer
Google에서 발표한 Attention All You Need에서는 GPU 병렬 계산을 못하는 단점을 보완한 Transformer라는 모델을 제시한다.
논문에서 말하는 구조는 아래와 같다.

Transformer의 특징
- RNN 기반 모델을 전부 제거
- Positional encoding을 통한 위치 정보 추가
- Self Attention을 통한 Context Vector 생성
- Residual connection(skiped-connection)을 통한 다층 구조
- Multi-Head Attention을 통한 앙상블 효과
- Masked Self Attention을 통한 디코더 입력에서의 데이터 누수 방지
논문 제목에서 알 수 있는 것 처럼 RNN 구조를 전부 제거하고 Attention만 사용해서 병렬 처리를 가능하게 했다.
하나씩 알아보자.
1. RNN 기반 층을 전부 제거
seq2seq 모델에서 RNN 기반 층이 병렬 연산을 못하게 한다. Transformer는 이러한 RNN 층을 전부 제거해서 이러한 문제를 해결했다.
RNN을 제거하기 위해선 RNN이 쓰이게 된 이유를 알아야 한다. 또 어떤 방법을 써서 RNN이 하던 역할을 대신하게 했는지 알아야 한다.
간략하게 한 번 알아보자.
- 자연어 처리에서 RNN을 사용하게 된 이유
- 전통적으로 사용되던 통계적 언어모델의 한계인 희소성(Sparsity) 문제(횟수 기반으로 확률을 계산 때문에 학습하지 않은 내용은 생성이 불가능) 때문에 word2vec, fastText 등 word embedding을 활용하는 신경망 언어모델을 사용하기 시작
- 앞 단어와의 관계, 즉 단어의 순서에 따라 달라지는 의미를 반영하기 위해 사용
- "이것 저것 그 사람"과 같은 지시대명사의 의미를 반영하기 위해 필요
- RNN의 역할을 대신한 방법
- word embedding을 그대로 활용함
- Positional encoding을 통해 word embedding에 위치 정보를 더해서 단어의 순서를 반영
- Self Attention으로 전체 단어 사이의 유사도 확인을 통해 지시대명사 의미 파악
이렇게 정리할 수 있다.
RNN의 역할과 대신한 방법에 대한 설명이 아주 정확하진 않지만, 개인적으로는 이렇게 받아들이는 게 Transformer 이해에 도움이 되었다.
2. Positional encoding을 통한 위치 정보 임베딩
Positional encoding은 입력 문장의 단어 순서를 반영하기 위해 제안된 방법이다.
이것을 하지 않으면 순서 정보가 반영되지 않기 때문에 sequence형 데이터를 제대로 처리할 수 없게 된다.
따라서 Transformer에서는 특정 정보를 입력 임베딩 벡터에 더해 상대위치, 혹은 절대위치를 반영할 수 있게 하였다.
논문에서 제안한 방식은 아래와 같다.
$PE_{(pos,2i)} = \displaystyle sin\left(\frac {pos}{10000^{\frac{2i}{d_{model}}}}\right)$
$PE_{(pos,2i+1)} = \displaystyle cos\left(\frac {pos}{10000^{\frac{2i}{d_{model}}}}\right)$
단어의 위치를 pos, word embedding 배열의 인덱스를 i 라고 보면 된다. $d_{model}$은 word embedding 배열의 차원이다. (※ 앞으로 쓰일 입력과 출력의 크기를 의미하기도 한다.)
주기함수인 sin과 cos을 이용해서 단어의 위치, 그리고 word embedding 배열의 인덱스 마다 서로 다른 값을 넣을 수 있다.
식을 약간 수정하면,
$PE_{(pos,i)} =\displaystyle\frac{(1+(-1)^{i})}{2}sin\left(\frac {pos}{10000^{\frac{i}{d_{model}}}}\right) + \displaystyle\frac{(1+(-1)^{i+1})}{2} cos\left(\frac {pos}{10000^{\frac{i-1}{d_{model}}}}\right)$
이렇게 한 줄로 표현 가능하다.
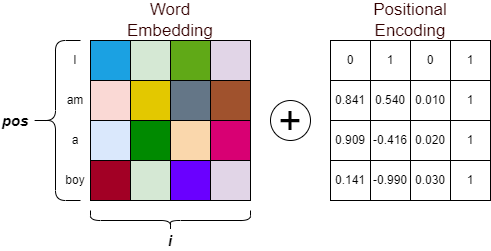
그림의 좌표 값, pos와 i를 위 식에 대입하면 더해야 할 Positional Encoding 값을 쉽게 구할 수 있다.
논문에서는 주기힘수 sin, cos을 사용하지 않고 positional encoding을 직접 학습해도 비슷한 결과가 나온다고 한다.
성능에 큰 차이가 없다면 computing power를 아끼기 위해서 위 식을 쓰는게 좋을 것 같다.
아래 그림은 Positional Encoding 계산 결과를 시각화 한 것이다.
[ pos = Position(y축), i = Depth(x축) ]

그림에서 보면 word embedding 배열의 앞 부분 부터 포지셔널 인코딩 값이 있는 것으로 보인다.(Depth 부분)
Position이 50이면, 입력된 문장의 길이가 50이라는 의미이고 Depth가 128인 의미는 word embedding의 차원이 128이라는 의미이다.
※ 생각해볼 문제
만약 입력 문장의 길이가 10이고 40만큼 패딩이 들어갔다면, 패딩을 앞에 두는게 유리할까 뒤에 두는게 유리할까?
직접 테스트를 통해 알아볼 예정이다.(혹시 아시는 분 있으시면 댓글 부탁드립니다!)
그럼 여기까지 설계하면 이렇게 된다.

입력을 한 번에 받기 때문에 LSTM에 비해 그림이 훨씬 단순해 졌다.
3. Self Attention을 통한 Context Vector 생성
Self Attention이 무엇일까?
기본적으로는 자기 자신과 Attention을 한다는 의미다.
Self Attention이 나온 이유는 기존 LSTM seq2seq 모델에서 사용된 Attention mechanism이 디코더의 Quary와 인코더의 Key를 Attention 하기 때문이다. Self Attention은 자기 자신의 Quary와 Key를 Attention 한다.
말이 조금 어렵다. 그림으로 보면 조금 더 쉽게 이해할 수 있다.
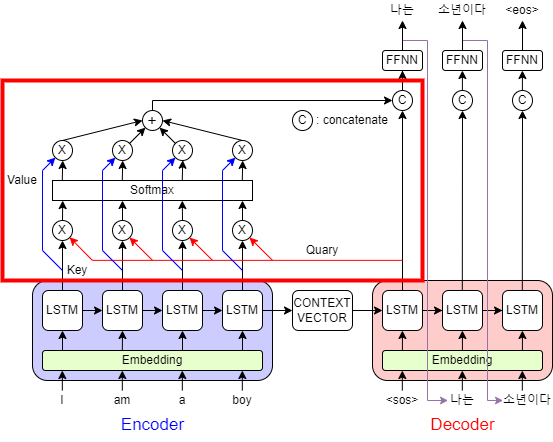
빨간색으로 테두리를 친 부분이 Attention 부분이다.
그림을 보면 디코더의 출력이 Quary로써 Attention으로 들어가는 것을 확인할 수 있다.
마찬가지로 인코더의 각 출력이 Key와 Value로써 Attention으로 들어가는 것을 확인할 수 있다.
이것을 Encoder-Decoder Attention이라고 부른다.
Self Attention은 Quary와 Key, Value의 출처가 같은 것을 의미한다.
아래 그림을 보자.

Self Attention을 간략하게 표현한 다이어그램이다. Quary, Key, Value가 모두 같은 입력으로 부터 들어간다.
이러한 Attention을 Self Attention이라고 한다.
이제부터 Self Attention에 적용한 Scaled Dot-product Attention 메커니즘에 대해 설명할 것이다.
Attention에 대해 제대로 이해하고 있다면 이 부분을 이해하기 쉬울 것이지만, 아니라면 조금 버거울 수 있다.
최대한 차근차근 설명해보겠다.

다소 복잡해 보인다. 하지만 하나씩 뜯어보면 의외로 간단한 구조다.
총 3개의 입력, Quary, Key, Value를 받아서 출력값 Z를 구하는 방식이다.
이때, Quary, Key, Value의 사이즈는 모두 동일하다.
$Z = Attention(Q, K, V ) = \displaystyle softmax\left(\frac{QK^T}{\sqrt{dk}}\right)V$
결국 위 식 하나로 간략하게 정리된다.
백문이불여일견, Self Attention 예시를 통해 Scaled Dot-product Attention이 어떻게 계산되는지 알아보자.
예시로 위에서 사용한 I am a boy의 워드 임베딩 값을 가져왔다.
좀 더 명확한 이해를 돕기 위해 입력 피쳐의 개수와 워드 임베딩의 차원 수를 다르게 바꾸었다.

예시 입력 X = (4 X 5) 행렬로 진행하겠다. 나중에 배치사이즈를 포함할 텐데, 지금은 배치 사이즈가 1이라고 생각하면 좋다.
Transformer에서 Attention은 입력 X를 받아서 Quary, Key, Value를 만들어주는 층이 하나 더 추가된다.

우선 Dense layer를 통과해서 Quary, Key, Value 값을 구해보자.
$W_Q$, $W_K$, $W_V$ 의 크기는 $(5 \times hs_{dim})$ 이 된다.
5는 입력 워드 임베딩 배열의 차원이고 $hs_{dim}$은 hidden state dimension으로 사용자가 정해주는 하이퍼파라미터이다.
차이를 두기 위해 $hs_{dim} = 3$으로 해 두겠다.

그 다음 Quary와 Key를 행렬곱 해준다.
둘의 사이즈가 같기 때문에 하나만 Transpose 하면 행렬곱을 할 수 있다.

(※ 첫 라인에 숫자가 적힌 것은 예시이다.)
이런식으로 자기 자신을 Quary와 Key로 사용한 후 Attention을 구한 것을 Self Attention이라고 한다.
계속해서 따라가보자.
다음은 scale이다. scale을 해주는 이유는 소프트맥스 함수를 사용하면서 발생하는 문제점 때문이다.
우선 $d_K$에 대해 알아보자. $d_K$는 Quary, Key, Value의 $hs_{dim}$, 즉 열 사이즈이다. 현재 $hs_{dim} = 3$으로 예시를 들었기 때문에 ( 4 X 3 ), 3이다.
Dot-product Attention에서 $d_K$가 작은 값이면 scale을 하나 안 하나 결과가 비슷하다. 하지만 $d_K$가 클 경우, 특정 값의 크기가 매우 커져 나머지 값들을 매우 작은 비율로 나오게 한다.
이는 소프트맥스를 사용하기 때문에 발생한다. 소프트맥수는 지수함수를 사용하기 때문에 $e^n$에서 n이 크면 클수록 다른 값 보다 조금만 커져도 굉장히 큰 비율을 가져간다.
예를 들어
[4, 2, 1.4, 3.6]
위에 예시로 적은 대로 이렇게 4개의 값이 있다고 해보자.
4와 3.6, 2와 1.4는 비슷하기 때문에 어느정도 확률을 비슷하게 가져야야 할 것이다.
그러나 소프트맥스 함수
$Softmax(z_i) = \displaystyle\frac{e^{z_i}}{\displaystyle\sum_k{e^{z_k}}}$
를 통하게 되면 각각
[4, 2, 1.4, 3.6] => [0.532, 0.072, 0.040, 0.357]
로 생각보다 차이가 많이 나는 결과를 얻게 된다.
소프트맥스 함수를 계산하기 전에 $\sqrt{d_K}$(여기선 $\sqrt{3}$)로 나누는 scale을 해주면,
[2.31, 1.15, 0.81, 2.08] => [0.429, 0.135, 0.096, 0.340]
위와 같이 차이가 조금 줄어들게 된다.
즉, $d_K$의 값이 너무 크다면 스케일링을 통해 특정 값이 지나치게 많은 확률을 가져가는 것을 방지할 수 있다.
scale과 softmax까지 통과하고 난 다음 식은 아래와 같다.
$Softmax\left(\frac{QK^T}{\sqrt{dk}}\right)$
그림으로 표현하면

이렇게 나타낼 수 있다.
마지막으로 Value와 행렬곱을 하게 되면

이런식으로 $Attention(Q,K,V) = Z$를 구할 수 있다.
이 $Z$가 Context Vector이다.
Context Vector $Z$의 최종사이즈는 예시에서 (4 X 3), 즉 $(\# feature \times hs_{dim})$ 이다.
위 여기까지 블록다이어그램을 그리면 아래와 같다.

입력이 (4 X 5)가 들어와서 출력 (4 X 3)이 나왔다.
$hs_{dim}$ 값에 따라 입력과 출력의 사이즈가 달라진다는 사실을 기억하자.
4. Residual connection(skiped-connection)을 통한 다층 구조
이제 Scaled Dot-product Attention을 통해 Self Attention을 구현하는 것을 배웠다.
하지만 Transformer는 여기서 끝이 아니다.
Transformer는 Encoder를 여러층 쌓는 다층 구조를 사용하고 있다.
이를 위해서 2015년 ILSVRC에서 우승한 ResNet의 Skipped Connection 구조를 차용했다.
Skipped Connection은 ResNet에서 처음 사용되었기 때문에 Residual Connection이라고도 한다.

$X_l = X_{l-1} + F(X_{l-1})$
위와 같이 표현할 수 있다.
입력 X 값을 다음 층의 결과와 더하는 방식이다.
이런 식으로 하면 층이 깊어져도 정보 손실을 최소화 할 수 있기 때문에 다층 구조를 가져갈 수 있다.
대신 입력 X와 출력 F(X)의 행렬의 사이즈가 같아야 한다.
하지만 3번의 결과에서 하이퍼 파라미터 $hs_{dim}$에 따라 입력과 출력 사이즈가 달라질 수 있다는 것을 알았다.
다층 구조를 쌓기 위해서 $hs_{dim}$을 입력 word embedding 배열의 차원과 맞춰주면 출력 결과 값도 같아질 것이다.
3번의 예시에서 $hs_{dim} = 5$ 로 두면 입력 (4 X 5), 출력 (4 X 5)로 사이즈가 같아진다.
그럼 아래와 같이 Skipped Connection을 연결할 수 있게 된다.

하지만 이렇게 되면 하이퍼 파라미터가 더 이상 하이퍼 파라미터가 아니게 된다.
이 문제를 해결하기 위해 Attention Is All You Need 논문에서 제안한 Multi-head Attention 구조에 대해 알아보자.
(※ 사실 이 문제 때문에 제안한 구조는 아니다. 하지만 이것으로 이 문제가 깔끔하게 해결된다.)
5. Multi-Head Attention을 통한 앙상블 효과
